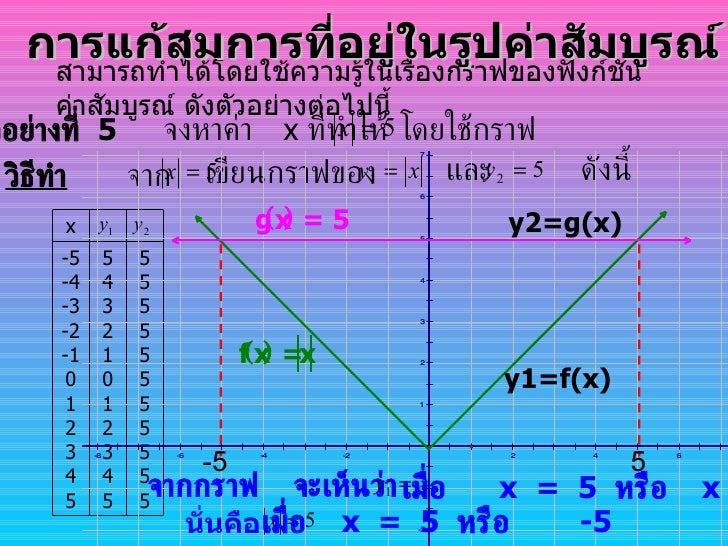
รูป ก,ง กราฟตัดแกน X 2 จุด คือที่จุด A และ จุด B รูป ข,ค กราฟตัดแกน X 1 จุด คือที่จุด P หรือสัมผัสแกน X ที่จุด P
รูป ค,ฉ กราฟไม่ตัดแกน X กราฟอยู่เหนือแกน X และใต้แกน X ตามลำดับ อ่านเพิ่มเติม
รูป ค,ฉ กราฟไม่ตัดแกน X กราฟอยู่เหนือแกน X และใต้แกน X ตามลำดับ อ่านเพิ่มเติม



(2).jpg)
(2).jpg)
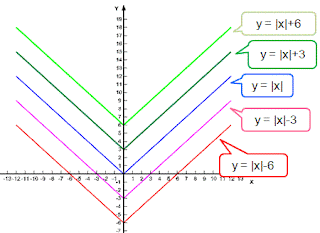
 เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ
เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ  ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ ดังรูป
ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ ดังรูป (2).jpg)
 และ
และ  คือ
คือ  , โดยที่ M คือ
, โดยที่ M คือ  จะเป็น การสายเส้นตรง ก็ต่อเมื่อ
จะเป็น การสายเส้นตรง ก็ต่อเมื่อ 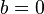 เท่านั้น
เท่านั้น (2).jpg)

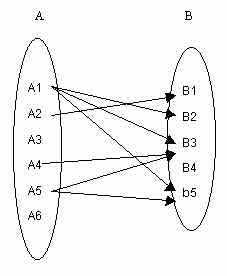
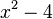 สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้น
เป็นต้น 






